二次函数的定义、注意事项及三种解析式表达方法详解
<股票配资网>二次函数的定义、注意事项及三种解析式表达方法详解
二次函数的定义
二次函数是指具有一般形式y=ax²+bx+c的函数二次函数的定义、注意事项及三种解析式表达方法详解,其中a、b、c是常数且a≠0。这样的函数被称为二次函数。请注意以下几点:
函数表达式必须为整式。
自变量x的取值范围是全体实数,且其最高次数为2。
在书写各项系数时,务必包含其前面的符号。例如,a是二次项系数,b是一次项系数,而c是常数项。
二次项系数a必须不等于0。
二次函数的解析式也可以被称作表达式或关系式。
二次函数解析式的三种表达方法
(1) 一般式:y = ax² + bx + c,其中a、b、c为常数且a≠0。
(2) 顶点式:y = a(x - h)² + k,其中a、h、k为常数且a≠0,且(h, k)为顶点坐标。
(3) 交点式(或称两根式、因式分解式):y = a(x - x₁)(x - x₂),其中a≠0,x₁和x₂是二次函数图像与x轴交点的横坐标,即一元二次方程ax² + bx + c = 0的两个实数根。
二次函数y = a(x - h)² + k与y = ax² + bx + c的图像和性质

二次函数表达式的确定
在给定条件下确定二次函数的表达式,通常采用待定系数法。由于二次函数存在三种不同的表达式,因此在应用待定系数法时,需根据题目条件谨慎选择合适的表达式进行设立,以便更高效地解决问题。
一般而言,以下情况适用不同的表达式:
若已知或能推导出二次函数图像上的三个点的坐标,通常选用一般式。
若已知或能推导出二次函数的顶点、对称轴或极值,则顶点式更为合适。
若已知或能推导出二次函数图像与x轴的两个交点的横坐标,或一个交点及对称轴,则交点式(或称两根式)更为适用。
对于已知或能推导出纵坐标相同的两点的二次函数二次函数的定义、注意事项及三种解析式表达方法详解,顶点式往往更为便捷。
二次函数图像的变换
(1)平移变换
函数的平移遵循统一规律:沿y轴上下平移时,只需在常数项上进行加减操作,这会影响函数图像与y轴的交点;而沿x轴左右平移时,则需在变量x上进行加减操作,这会改变函数图像与x轴的位置。例如,将二次函数图像y=ax²+bx+c沿x轴左移m个单位,再沿y轴上移n个单位,新的函数表达式将为y=a(x+m)²+b(x+m)+c+n;若将图像y=a(x-h)²+k沿x轴右移m个单位,再沿y轴下移n个单位,则新的表达式为y=a(x-h-m)²+k-n。
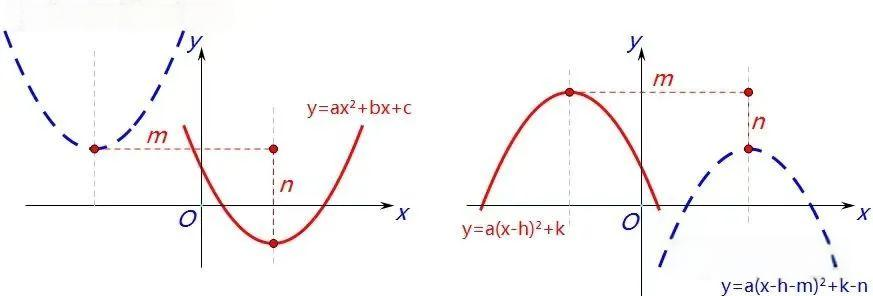
(2)二次函数的对称变换
关于x轴对称
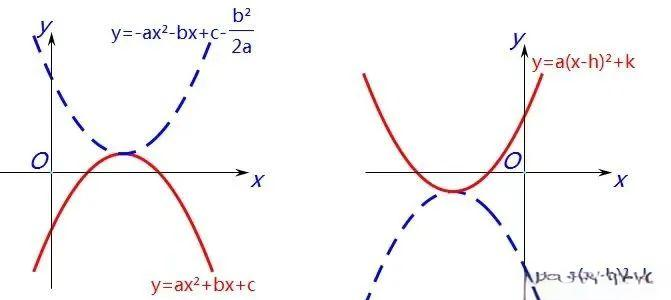
当二次函数图像y=ax²+bx+c关于x轴对称时,其开口方向会发生变化,同时与y轴的交点也会改变。因此,在解析式上,所有系数都会变号。对称后的函数表达式为y=-ax²-bx-c。
同样地,对于二次函数图像y=a(x-h)²+k,关于x轴对称后的表达式则为y=-a(x-h)²-k。
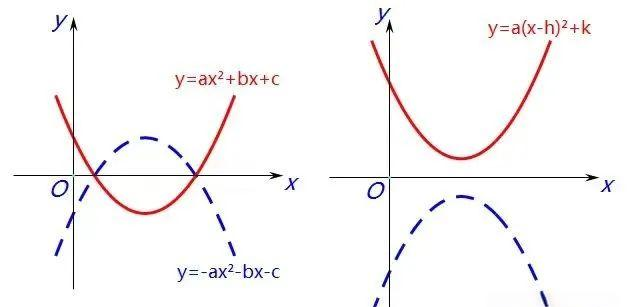
关于y轴对称
当二次函数图像y=ax²+bx+c关于y轴对称时,其开口方向保持不变,与y轴的交点也维持原样。然而,由于对称轴发生了变化,因此在解析式上,只有中间项的系数发生了变号。对称后的函数表达式为y=ax²-bx+c。

同样地,对于二次函数图像y=a(x-h)²+k,关于y轴对称后的表达式则为y=a(x+h)²+k。
关于原点对称
当二次函数图像y=ax²+bx+c关于原点对称时,其开口方向会发生变化,同时与y轴的交点也会改变。因此,在解析式上,所有系数的符号都会发生改变,即变为相反数。对称后的函数表达式为y=-ax²+bx-c。
同样地,对于二次函数图像y=a(x-h)²+k,关于原点对称后的表达式则为y=-a(x+h)²-k。

关于顶点对称
对于二次函数图像y=a(x-h)²+k,当其关于顶点对称时,函数表达式会变为y=-a(x-h)²+k。
关于点(m,n)对称
当二次函数图像y=a(x-h)²+k关于点(m,n)对称时,其函数表达式会发生变化。具体来说,对称后的解析式为y=-a(x+h-2m)²+2n-k。这一变化体现了函数图像在平面上的对称性质。
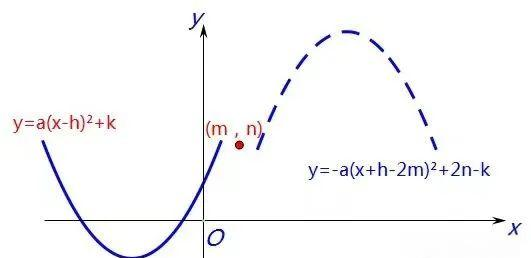
对于选择题和填空题,可直接利用变换口诀写出表达式。
对于需要详细解答的题目,关键在于理解线的对称与平移本质上都是点的对称与平移。首先,确定原二次函数(或已知解析式的二次函数)上的三个关键点,然后求出这三个点关于对称中心或平移后的对应点。最后,通过这些变换后的点,写出变换后的二次函数解析式。
在平移过程中,抛物线的开口方向和形状保持不变,因此a的值始终保持不变。而在对称过程中,抛物线的形状同样不会改变,所以|a|也始终保持不变。
接下来,我们探讨二次函数图像与系数之间的关系。首先,根据a的符号可以判断开口方向。其次,通过b的符号与a的符号可以判断对称轴的位置,常用方法是“左同右异”,即对称轴在y轴左侧时,a和b同号;在右侧时,a和b异号。再次,c的符号决定了函数图像与y轴交点的位置,交点在y轴正半轴时c为正二次函数待定系数法,负半轴时c为负。此外,判别式=b²-4ac可以用来判断函数图象与x轴的交点个数。若判别式为负,则无交点;为0时有一个交点;为正时有两个交点。
另外,如果a和b的系数之间存在平方关系,例如需要判断a+b+c、a-b+c、4a+2b+c或9a+3b+c的符号,可以通过取特殊值的方法来解决,例如令x=-1或3来代入解析式。
最后,我们介绍如何根据二次函数解析式来比较大小。这可以通过比较点到对称轴的距离和抛物线的开口方向来实现(画简图辅助理解)。在图1中,由于d1y2。

利用抛物线对称轴解题(看到纵坐标相等时,思考其关于对称轴的对称性)
在解决与抛物线相关的问题时,我们经常需要利用其对称性。当遇到纵坐标相等的点时,我们可以考虑它们关于抛物线对称轴的对称性。这种思路在解题过程中非常有用二次函数待定系数法,可以帮助我们更快地找到答案。
求解二次函数y=ax²+bx+c的最值方法
在数学中,二次函数是一种常见的函数类型,其一般形式为y=ax²+bx+c。这类函数具有特定的性质,包括对称性和最值。为了找到二次函数的最值,我们可以利用其图像和性质进行求解。具体方法包括完成平方、找出对称轴,以及利用导数等数学工具。通过这些方法,我们可以轻松地找到二次函数的最值。
解决交点问题
在数学领域,交点问题是一个常见且重要的研究课题。它涉及到寻找两个或多个函数、曲线或图形的交点,这些交点可能代表着特定的条件或关系。为了求解交点,我们可以利用代数方法、几何直观以及数值计算等策略。通过这些方法,我们可以深入探索交点问题的本质,并找到相应的解决方案。

关键洞见
在深入研究交点问题的过程中,我们得出了一些重要的结论。这些结论不仅揭示了交点问题的内在规律,还为我们提供了求解交点的新思路和新方法。通过这些关键洞见,我们能够更准确地把握交点问题的本质,从而找到更有效的解决方案。

利用二次函数图像求一元二次方程的近似解
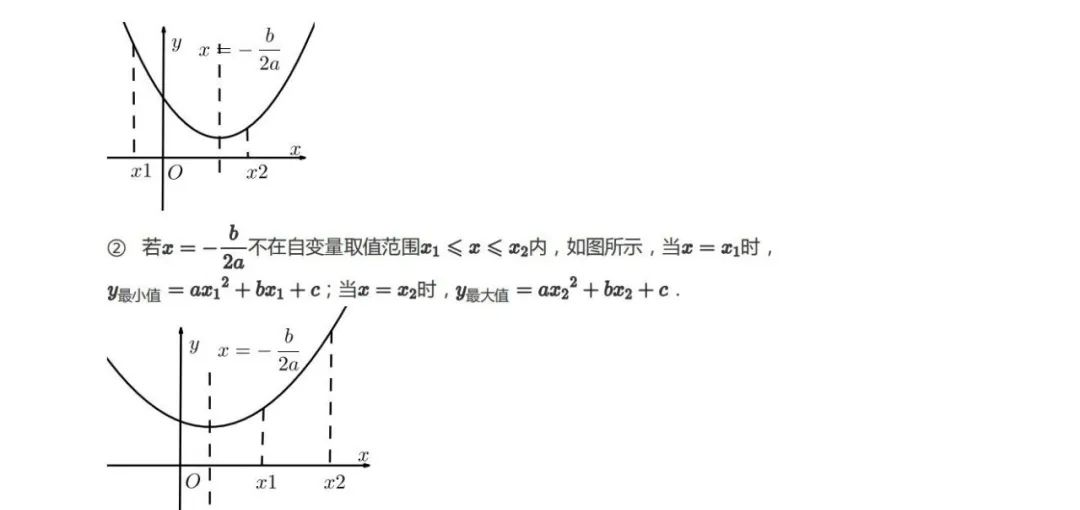
对于二次函数y=ax²+bx+c(其中a≠0),当x取值为x₁和x₂(且x₁